THE SHIELD OF ACHILLES

By Dr S. A. Paipetis, Professor Emeritus of University of Patras

Achilles, succumbing to the pleas of the Achaeans, who were facing defeat in his absence, sent his friend Patroclus to fight in his stead, wearing Achilles΄ own panoply, to deceive the Trojans and make them think that Achilles himself had returned to battle. However, Patroclus was killed by Hector, and Achilles lost, besides his friend, his panoply as well. So he was unarmed, when, enraged, he truly wanted to return to war. Thetis, his mother, visited Hephaestus and asked him to fashion a panoply for her son.

Fig. 1 Thetis receiving Achilles’ panoply from Hephaestus, [Tate Gallery, London, Sir James Thornhill (1675-1734)].

In Book XVIII of the Iliad, the construction of Achilles΄ panoply by Hephaestus is described. In particular, in v. 474-482, immediately after the reference to Hephaestus΄ “bellows”, Chapter 12, a purely technical account of the manufacture of Achilles’ shield is given:

(Hephaestus…)

threw tough copper into the fire, and tin, with silver and gold; he set his great anvil on its block, and with one hand grasped his mighty hammer while he took the tongs in the other. First he shaped the shield so great and strong, adorning it all over and binding it round with a gleaming circuit in three layers; and the baldric was made of silver. He made the shield in five thicknesses, and with many a wonder did his cunning hand enrich it.

(Iliad, 18: 474-482)

This description corresponds to a multi-layered structure, consisting of five successive metal laminates with very different mechanical properties. In particular, the shield consists of two external laminates of hard bronze, two internal ones of tin and a central laminate of pure, i.e., soft, gold. This structure exhibits maximum resistance to penetration, as proved by a complete numerical simulation of large-strain elasto-plastic behaviour when impacted by the tip of a piercing element, such as the spear-like head of an arrow. The analysis and parametric study of the problem, have most accurately confirmed the Homeric descriptions of the battle behaviour of the shield and revealed important elements of advanced technology in Mycenaean times, disguised as the miraculous power of gods.

Fig. 2 Sketch of an eight-shaped shield and its representation on a mosaic.

Mycenaean shields appear in various shapes, mainly as eight-shaped (Fig. 2), circular (Fig. 3,4) or full-body shields. Note the representations of ghastly beings on the shields, aiming to intimidate the enemy.

Fig. 3 Typical geometry of a circular Mycenaean shield.
(12^th century BCE).

The Homeric description classifies Achilles΄ shield as circular. Numerous reconstructions of it have been made (Fig. 5), especially reproducing its decorations, which are accounted for in detail in Il. 18.483-608. Out of those, the excellent reconstruction in gold by Philip Rundell (1821) on the coronation of King George IV, is distinguished (Fig. 6).

Fig. 4 Typical decorated shields of the Homeric era.

Fig. 5 Two representations of Achilles΄ shield based on the Homeric description.

The battle behaviour of the shield of Achilles is described in the Iliad on three distinct occasions.

(a) The duel between Achilles and Aeneias:

‘…The son of Peleus

held the shield before him with his strong hand, and he was afraid, for he deemed that Aeneas’s spear would go through it quite easily, not reflecting that the god’s glorious gifts were little likely to yield before the blows of mortal men; and indeed Aeneas’s spear did not pierce the shield, for the layer of gold, gift of the god, stayed the point. It went through two layers, but the god had made the shield in five, two of bronze, the two innermost ones of tin, and one of gold; it was in this that the spear was stayed….’

(Iliad, 20: 260-270)

(b) The duel between Achilles and Hector:

‘…He poised his spear as he spoke and hurled it. His aim was true for he hit the middle of Achilles’ shield, but the spear rebounded from it, and did not pierce it…’

(Iliad, 22: 290-292)

Thus did he defy him, and Achilles raised his spear of Pelian ash. Asteropaeus failed with both his spears, for he could use both hands alike; with the one spear he struck Achilles’ shield, but did not pierce it, for the layer of gold, gift of the god, stayed the point;

(Iliad, 21: 61-164)

These references are highly enlightening and provide a basis for numerical simulation of the weapon, i.e., of a spear with a hard bronze tip impacting the shield. The exact geometry of the shield and the spear are not known, but based on archaeological findings and the schematic or painted representations, fundamental information for the analysis has been obtained. The geometry of the shield is shown in Fig.6, while a number of typical bronze spearheads appear in Fig. 7.

Fίg. 7 Characteristic decorated spear-heads used in the Trojan War.

Numerical analysis and results

Assume that each of the five laminates of Achilles΄ shield is 1.5 mm thick, i.e., the shield is 7.5 mm thick. Considering a spear hitting it at its centre in a direction normal to the surface, an axisymmetric problem results. In Fig. 8, details of the shield cross section are given along with its three-dimensional discretization. The form of the generatrix of the shield cross section is elliptic with semi-axes 300 and 120 mm respectively. This leads to a total mass of 16.75 kg. The spear is a rod 2.2m long with 16 mm diameter.

The form of spear tip was based on vase paintings and archaeological findings. As often described in the Iliad, bronze spearheads were fastened on long wooden rods with circular cross section. The dimensions and materials of the spear correspond to a total mass of 3.25 kg. As stated, the shield was studied as a multi-layered structure, and the way in which the laminates were interconnected was a key-point.

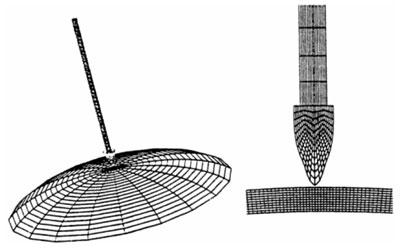Fig. 8 Finite Element discretization of the spear-shield system: The complete three-dimensional model (left) and a detail of spearhead (pike) and shield contact point (right).

Furthermore, it was assumed that the edges of the front laminate were turned backwards, encasing the whole structure. In addition, a number of bolts kept the laminates together across the thickness, securing good mechanical cooperation. The number and arrangement of the bolts is very important for the impact response of the shield and stress distribution.

In the present analysis, it was assumed that the bolts were arranged circumferentially on a circle at 120 mm distance from the shield axis of symmetry. Such an arrangement allows the laminates to slide in relation to each other.

The spear velocity was taken equal to 20 m/sec. Two specific cases were studied. In the first, all shield laminates consisted of hard bronze (or “copper”), while, in the second, the true (according to Homer) formation of the shield is considered, e.g., two external bronze laminates, two internal tin laminates and a central laminate of gold. The spearhead consists of hard bronze.

Fig. 9 Impact behaviour of the spear-shield system, with all shield’s laminates being of bronze, at 4 msec time after contact, by which the spear penetrates the shield.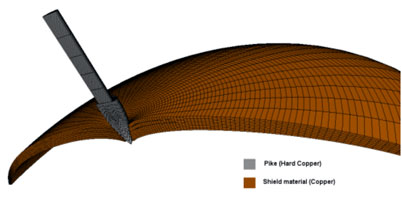

In Fig. 9 the response of the shield when all laminates were of bronze is presented. In this case, the spear penetrates the shield. In Figs. 10 and 11 the respective displacement and velocity diagrams of spear tip and the central point of the shield are plotted against time. Penetration of the shield is complete after 4 ms, while the change in slope of the velocity diagram of the spear tip corresponds to the ensuing penetration into the bronze laminates. At the end of the penetration stage, the spear has almost zero velocity, while the shield displacement reaches 35 mm.

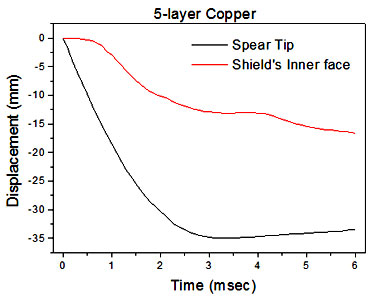Fig. 10 Displacement diagrams of spear tip and of the central point of the shield plotted against time, when all shield’s laminates are of bronze (5 bronze – or “copper” – laminates).

Fig. 11 Velocity diagram of spear tip and of the central point of the shield plotted against time, when all shield’s laminates are of bronze (5 bronze – or “copper” – laminates).

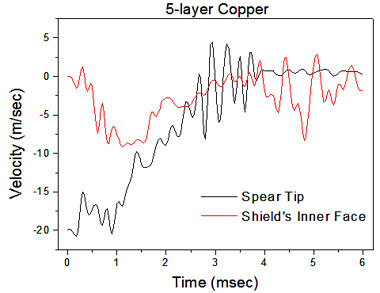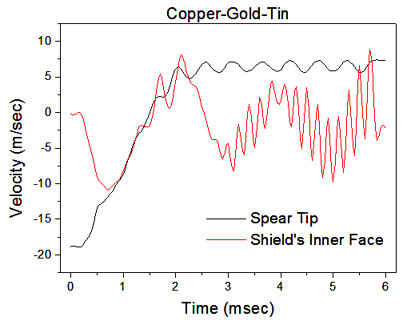
Fig. 12 presents the response of the simulated Achillesʼ shield. In this case, the spear tip stopped at the gold laminate, having pierced the two external bronze and tin laminates. This occurs within 1.5 msec, while, in the sequence, the spear rebounded. Fig. 13 presents velocity diagrams of the spear tip and the shield’s central point respectively plotted against time.

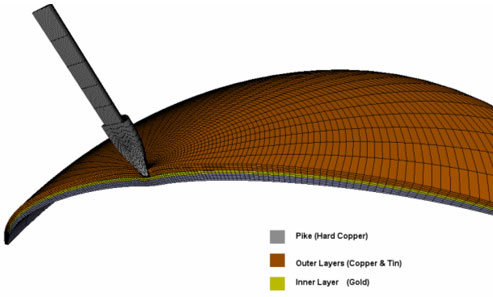
Fig. 12 Impact behaviour of spear-shield system based on the real properties of the individual shield laminates (bronze-tin-gold) at 1.5 msec time, in which case the spear penetrates the two external laminates, i.e., bronze and tin, and is stopped by the gold laminate.

Fig. 13 Velocity diagrams for spear tip and the central point of the shield by using the “real” materials (bronze-tin-gold) of Achilles’ shield.

In conclusion, one can note that:

(a) The shield consisted of a layering of laminates with very different mechanical properties, of which the strongest was hard bronze.

(b) The combination of these materials, in the way described in the Iliad, prevented the spear from penetrating the shield, since, on one occasion, it was repulsed and rebounded, while, on the other, it only pierced the first two laminates (bronze-tin) and subsequently it was stopped by the gold laminate.

(c) If all laminates of the structure consisted of bronze, under the same impact conditions, the shield would be penetrated.

This fact is due to the complete difference in behaviour of the materials under static and dynamic loading. The object of a defensive device, like a shield, is to “destroy” (in fact to scatter) the kinetic energy of the projectile, by converting it into heat, and not just to sustain a large static load. This ability is not possessed by hard bronze itself, exhibiting very small deformations in relation to the rest of the materials and also possessing very low damping properties. On the contrary, tin but, mainly, pure (i.e., soft) gold, while undergoing plastic deformation, causes attenuation of the motion by dissipating the kinetic energy of the spear. Moreover, the laminated structure contributes a certain amount of damping due to friction between the laminates, which, however, is not the main energy dissipation mechanism.

* * *

Based on these remarks, the hypothesis that the shield manufacturer possessed deep knowledge of the dynamic mechanical properties of laminated composite structures, essentially nearly modern structural elements, is fully confirmed.

Freeinquiry